Előadás 3
Ha a Föld szigorúan gömbölyű egy egységes sűrűségeloszlással, akkor a gravitációs potenciálja egybeesne egy olyan anyagpont potenciáljával, amelynek tömege megegyezik a Föld tömegével. Ebben az esetben a műhold a Kepler törvényei szerint mozogna:
Kepler első törvénye: A műhold pályája a második rend görbének (kör, ellipszis, parabola), amelynek egyik fókája a vonzó test tömegének középpontja.
A Föld körül repült műholdak ellipszis pályán vannak. Az ellipszis a pontok lókuszpontja, az egymástól a két pontig terjedő távolságok összege, az úgynevezett fókusz, állandó érték, amely egyenlő a 2a-val, ahol a az ellipszis semimajor tengelye.
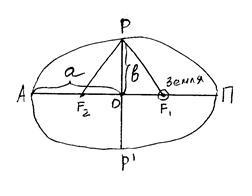
Az F1 és az F2 egy ellipszis középpontja
A-apogé (a műhold
a legnagyobb magasság a talaj felett)
P-perigé (a műhold
a legalacsonyabb magasság a Föld felett).
Második Kepler-törvény: A műhold sugárvektorának azonos időintervallumai egyenlő területeket írnak le. Ha t1 = t2. akkor S1 = S2. A rajz szerint: az idő t1 idő hosszabb, mint a t2 idő. ezért a perigé közelében lévő műhold sebessége nagyobb, mint az apogéne közelében.
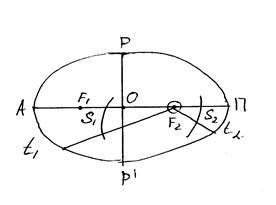
A műhold sugárvektorával leírt ábra az ágazat. Ezért a Kepler 2. törvénye szerint a műhold szektorsebessége állandó.
Kepler harmadik törvénye. A műhold forradalmi időszakának négyzetének aránya az orbit félhomály tengelyének kockájához a konstans érték:
Ha azt feltételezzük, hogy a műhold a Kepler törvényei szerint kering a pályára, akkor egy ilyen mozzanatot zavartnak neveznek.
A valóságban a műhold mozgása a pályán nagyon bonyolult. Különböző perturbáló erők működnek. A mesterséges műhold mozgását ebben az esetben megzavarták.
A szatellitek zavartalan mozgása.
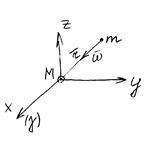
Feltételezzük, hogy a műhold tömeges tömegű m. Ha a műhold mozgása zavart, akkor a Földet is anyagi pontként vesszük a M. tömeggel. Figyelembe véve, hogy m "M, akkor tekinthető úgy, hogy a műhold nem vonzza a Földet, i.e. van egy "nulla tömeg".
A műhold zavartalan mozgásának differenciálegyenletének meghatározásához válasszuk ki az inerciális koordináta-rendszert (vagyis a forgó Földhöz viszonyítva).
Ha figyelembe vesszük más erők hatását, mint a Föld és a műhold kölcsönhatását, a műhold zavartalan mozgásának differenciálegyenletének származtatása az úgynevezett két testprobléma megoldására korlátozódik.
Aztán, figyelmen kívül hagyva a műhold működését a Földön, fontold meg a gyorsítást # 969, amely a földet a gravitációs törvény miatt a műholdra állítja.
Newton második törvénye szerint:
ahol az F erő megfelel
a gravitáció törvényével:
f a gravitációs állandó
# 964, - a műhold geocentrikus sugárvektorja.
Ahol f * M = # 956; - a gravitációs paraméter
Az (1) # 969; - gyorsulás, azaz. az út második származéka az időben, ezért;
Fontolja meg a koordináta-tengely mentén a gyorsulást:
; ;
Ezeknek a mennyiségeknek a megtalálásához az (1) egyenlet jobb oldalát kell szaporítani a # 945 irányú koszorúkkal, - az OX tengely mentén, # 946; - az OS tengely mentén, # 947; - az OZ tengely mentén) :; ; ; majd
A (2) képletek egy mesterséges műhold zavartalan mozgásának differenciálegyenletei.