Módszer Ljapunov függvények
Meghatározása Ljapunov függvény
Ljapunov függvény egy skalár függvény a fázis helyet a rendszer, amelyet fel lehet használni, hogy bizonyítani a stabilitását az egyensúlyi helyzet. Ljapunov függvény módszert alkalmazzák, hogy tanulmányozza a stabilitás a különböző differenciálegyenletek és rendszerek. Az alábbiakban arra szorítkozunk, hogy autonóm rendszerek \ [= \ mathbf \ left (\ mathbf \ right) \; \; \ text> \; \; >>> = \ left (,, \ ldots,> \ right),> \; \; \] A nulla egyensúlyi helyzet \ (\ mathbf \ ekvivalens \ mathbf. \)
Tegyük fel, hogy egy bizonyos környéken \ (U \) eredetű adott egy folyamatosan differenciálható függvény \ [V \ bal (\ mathbf \ right) = V \ bal (,, \ ldots,> \ jobbra). \] Legyen \ (V \ balra (\ mathbf \ right)> 0 \) minden \ (\ mathbf \ U \ backslash \ left \<\mathbf \right\>,\), És a származási \ (V \ balra (\ mathbf \ right) = 0. \) Az ilyen funkciók, például működik az űrlap \ [,> \ right) = ax_1 ^ 2 + bx_2 ^ 2> \; \ ; ,> \ Right) = ax_1 ^ 2 + bx_2 ^ 4> \; \; 0.> \] Most találtunk a teljes differenciálhányados \ (V \ balra (\ mathbf \ right) \) Idő \ (t: \) \ [>> = \ frac >>> \ frac >>> + \ frac >> > \ frac >>> + \ cdots> + >>> \ frac >>>> \] Ez a kifejezés felírható skalár szorzata két vektor :. \ [>> = \ left (\, V, \ frac >> >> \ right) \; \; \ text \; \; >>>> \ frac >>> \ ldots, \ frac >>>> \ right),> \; \; >>> = \ bal (>>>, \ frac >>>, \ ldots, \ frac >>>> \ jobbra).> \] Itt, az első vektor egy gradiens funkció \ (V \ balra (\ mathbf \ jobbra), \) t .e. ez mindig irányul az irányt maximális növekedése a függvény \ (V \ balra (\ mathbf \ jobbra). \) Általában, egy függvény \ (V \ balra (\ mathbf \ right) \) növekszik a távolság a eredetű, azaz, azzal a feltétellel, \ (. \ left | \ mathbf \ right | \ to \ infty \) A második vektor skalár szorzata - a vektoros sebesség. Bármikor, ez irányul érintőlegesen a fázis pályára.
Vegyük azt az esetet, amikor a származékot \ (V \ balra (\ mathbf \ right) \) a környéken \ (U \) a származási negatív: \ [\ frac >> = \ left (\, V, \ frac >>>> \ right) 0 \) minden \ (\ mathbf \ U \ backslash \ left \<\mathbf \right\>\);
\ (V \ balra (\ mathbf \ right) = 0 \);
stabilitási tételek
Tétel a stabilitását abban az értelemben, Ljapunov. Ha egy olyan környéken \ (U \) nulla megoldások \ (\ mathbf = \ mathbf \) autonóm rendszer létezik Ljapunov függvény \ (V \ balra (\ mathbf \ jobbra), \) az egyensúlyi helyzet \ (\ mathbf = \ mathbf \ ) van Ljapunov stabil.
A tétel a aszimptotikus stabilitását. Ha egy olyan környéken \ (U \) oldatok nulla \ (\ mathbf = \ mathbf \) van egy autonóm rendszer a Ljapunov függvény \ (V \ balra (\ mathbf \ right) \) negatív határozott származékot \ (>> \ normalsize> 0 \).
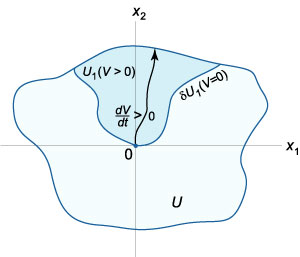
Ha a környéken \ (U \) vannak pontok, ahol a \ (V \ balra (\ mathbf \ right)> 0, \), majd a homogén oldatot \ (\ mathbf = \ mathbf \) nem stabil. Tétel Chetaev az instabilitás. Tegyük fel, hogy a környéken \ (U \) nulla megoldások \ (\ mathbf = \ mathbf \) autonóm rendszer, van egy folyamatosan differenciálható függvény \ (V \ balra (\ mathbf \ jobbra). \) Legyen a környéken \ (U \) tartalmaz egy aldomain \ ( \), beleértve a származási (ábra. \ (3 \)) úgy, hogy
\ (V \ left (\ mathbf \ right)> 0 \) minden \ (\ mathbf \ in \ backslash \ left \<\mathbf \right\>\);
\ (V \ balra (\ mathbf \ right) = 0 \) minden \ (\ mathbf \ in \ delta, \), ahol \ (\ Delta \) jelentése a határoló kistérségek \ (\).
Ezután a nulla oldatot \ (\ mathbf = \ mathbf \) a rendszer instabil. Ebben az esetben a fázis pályákat a aldomain \ (\) törekszik a eredetű.
Így a Liapunov funkció lehetővé teszi, hogy létrehozza a stabilitását, illetve instabilitását a rendszer. A módszer előnye, hogy nincs szükség tudni, hogy a döntés maga \ (\ mathbf \ left (t \ right) \.) Ezen túlmenően, ez a módszer lehetővé teszi számunkra, hogy vizsgálja meg a stabilitást az egyensúlyi pozíciók instabil rendszerek - például abban az esetben, ha a mérleg pont központ. Hátránya, hogy nincs általános módszert alkalmaztuk, Ljapunov függvények. Abban a különleges esetben a homogén autonóm rendszerek állandó együtthatók Ljapunov függvény megtalálható formájában kvadratikus formában.