Típusú nemlineáris differenciálegyenletek az 1. rendű
Leírás: A differenciálegyenletének egyenlete az értéke néhány ismeretlen funkciójú bizonyos ponton, és az értéke annak származékai különböző rendű ugyanazon a ponton. A differenciálegyenlet tartalmazza a funkciója ismeretlen és származékai a független változók egy linket; de nem tartalmaz semmilyen egyenlet származó ismeretlen funkció egy differenciálegyenlet. A nemlineáris differenciálegyenlet, vagy egy közönséges differenciálegyenlet részleges származékok, amelyekben legalább az egyik.
Fájl mérete: 163,25 KB
Job letöltve: 39 fő.
Ha ez a munka elérte az az oldal alján van egy lista a hasonló munkák. Is, akkor a keresés gombra
PSU elemzi. TG Sevcsenko
Típusú nemlineáris differenciálegyenletek az 1. rendű
211 diákcsoportok
Igor A. Birt
1. Bevezetés 3. oldal.
2. típusai differenciálegyenletek 4 o.
3. Gyakorlati rész 8. pp.
4. Hivatkozások 20 p.
differenciálegyenlet # 151; egyenlete az értéke néhány ismeretlen funkciójú bizonyos ponton, és az értéke annak származékai különböző rendű ugyanazon a ponton. A differenciálegyenlet tartalmazza az ismeretlen funkciót, annak származékai, és a független változók egy linket; de nem olyan egyenletet tartalmazó származékai ismeretlen funkciójú, egy differenciálegyenlet.
Az, hogy a differenciálegyenlet # 151; A legmagasabb rendű származékok szerepelnek benne.
A folyamat megoldani egy-egy differenciálegyenlet nevezzük integráció.
Minden a differenciálegyenletek osztható lineáris és nem lineáris.
A nemlineáris differenciálegyenlet - a differenciálegyenlet (rendes vagy részleges), hogy egy GR Roe legalább az alján a származékok az ismeretlen funkció (beleértve a nulla-rendű származékot - önmagában ismeretlen funkció) tartalmazza nemlineáris.
Néha alatt N.D.U. Arra utal, hogy a legtöbb általános egyenlete egy bizonyos típusú. Pl. nelineynymobyknovennym differenciálegyenlet 1 - sorrendben nevezzük. egyenlet tetszőleges
funkció a lineáris közönséges differenciálegyenlet az 1. rendű megfelel a konkrét esetben
N. d. Y. részleges 1. Ahhoz, hogy az ismeretlen függvény z
A független változók a következők:
ahol F - tetszőleges függvénye érvek;
Típusú nemlineáris differenciálegyenletek az 1. szabály:
Egyenleteket külön változók
Közönséges differenciálegyenlet
Létezik egy funkció u (x, y). hogy
A teljes szerves egyenlet teljes eltérés u (x, y) = C
u függvény ábrázolható formájában
ahol P (x, y). Q (x, y) - homogén függvény azonos mértékben
Behelyettesítve y = UX. dy = xdu + udx homogén egyenletet lefordítva lineáris függvény vonatkozásában u.
1. Ha a vonalak és pontban metszik egymást
(X 0; y 0), akkor helyette vezet homogén egyenlet
2. Ha az egyenes és párhuzamos, a csere eredményeképpen egyenlet többváltozós
Helyettesítés csökkenti a lineáris
Ha tudja, hogy bármelyik döntéseket. Az egyenlet redukálódik
Deriválva X és feltételezve, hogy az y „= p. Azért jöttünk, hogy egy lineáris egyenlet x függvényében p.
- Egy konkrét esetben a Lagrange egyenletek.
Hogy oldja meg a differenciálegyenlet
Ez az egyenlet a legegyszerűbb Riccati-féle egyenlet állandó együtthatós. A változók x, y könnyen szétválaszthatjuk, úgy, hogy az általános megoldás a következőképpen definiálható:

Oldjuk meg az egyenletet Riccati-féle
Arra törekszünk, egy adott oldat formájában:
Behelyettesítve ezt az egyenlet, azt találjuk:
Kapunk egy másodfokú egyenlet c:
Mi lehet választani bármilyen érték c. Tegyük fel például, hogy c = 2. Most, hogy tudod, egy adott megoldást, hogy a változás:
Ismét helyettesíteni ezt az eredeti Riccati-féle egyenlet:
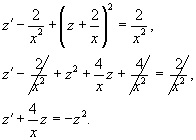
Mint látható, van egy Bernoulli-egyenlet paraméterrel m = 2. Tegyük újabb változás:
Osszuk a Bernoulli egyenlet Z2 (feltételezve, hogy z ≠ 0), és írd át a változó v:
Az utolsó egyenlet lineáris, és könnyen megoldható segítségével integráló tényező:
Az általános megoldás a lineáris egyenlet által meghatározott funkciót
Most majd következetesen visszatér az előző változókat. Mivel Z = 1 / v, az általános megoldás z van írva a következő:
Akkor nevezd állandó: 3C = C1 és írd a választ formájában
ahol C1 - tetszőleges valós szám.
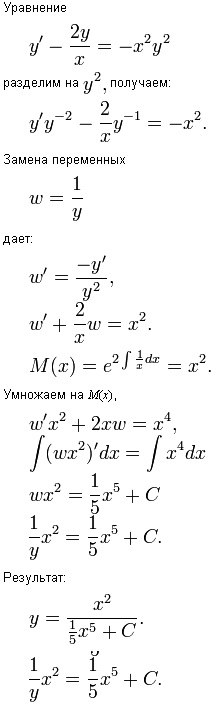
Találd meg az összes megoldást a differenciálegyenlet
Ez az egyenlet egy frakcionált paraméter Bernoulli
m = 1/2. Ez lehet csökkenteni lineáris differenciálegyenlet helyett
Purinszármazékban új funkció z (x) egyenlő
Elosztjuk az eredeti Bernoulli-egyenlet
Hasonlóképpen, más példák a weboldalon, a gyökér y = 0 is triviális megoldás a differenciálegyenlet. Ezért tudjuk írni:
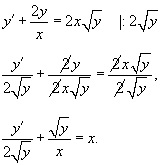
Behelyettesítve a y z. találunk:
Tehát, van egy lineáris egyenlet a függvény z (x). Integráló tényező leírásban egyenlő
Úgy döntünk, mint integráló tényező függvényében u (x) = x. Lehetőség van annak igazolására, hogy szorzást követően u (x) a bal oldalon az egyenlet lesz származtatott munkát z (x) u (x):
Ezután az általános megoldás egy lineáris differenciálegyenlet határozza meg a kifejezés:
Visszatérve az eredeti funkciója y (x), írunk az oldatot implicit formában:
Tehát a teljes válasz a következő:
Egyenletek elkülöníthető változók
Találd meg az összes megoldást a differenciálegyenlet
Transzformációs egyenlet az alábbiak szerint:
Nyilvánvaló, hogy a felosztást e y nincs veszteség megoldásokat például az e y> 0. integrációs megkapjuk
Ez a válasz lehet kifejezni kifejezetten:
Az utolsó kifejezés azt feltételezzük, hogy konstans C> 0, hogy megfelel a domain a logaritmikus függvény.
Keressen egy partikuláris megoldás, ha
Írja át az egyenletet az alábbiak szerint:
Osszuk mindkét oldalán 1 + e x.
Mivel 1 + e x> 0, akkor az osztály már nem vesztett döntéseket. Integrálása a kapott egyenlet:
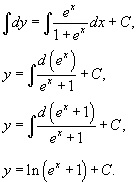
Most azt látjuk, a C konstans a kezdeti feltétel y (0) = 0.
Következésképpen a végleges válasz:
Keresse az általános és különös megoldást a differenciálegyenlet
Feltételezve, hogy y „= p, akkor felírható
Differenciálás, hogy x, azt találjuk:
Cserélje dy PDX:
Egyenlővé az első tényező nulla, ezt kapjuk:
Most helyettesíteni ezt a második egyenletbe:
Ennek eredményeként megkapjuk az általános megoldás az adott egyenlet Clairaut. Grafikailag ez a megoldás van ábrázolva egy paraméteres családja egyenes vonalak. Egyenlővé nullára a második tényezőt találunk más megoldást:
Ez az egyenlet megfelel egy adott megoldást a differenciálegyenlet és paraméteres formában van írva, mint
Kiküszöbölése p a rendszerből, a következő egyenlet integrál görbéből:
A geometriai szempontból, a parabola
Ez a boríték egy család egyenes vonalak által meghatározott általános megoldás.
Keresse az általános és különös megoldást a differenciálegyenlet
Bemutatjuk a paraméter y „= p:
Differenciálás mindkét oldalán úgy, hogy x az egyenletnek, megkapjuk:
Mivel dy = PDX, írhatunk:
Vegyük azt az esetet dp = 0. Ekkor p = C Behelyettesítve ezt az egyenletben, találni az általános megoldás:
Grafikailag ez a megoldás felel meg egy paraméteres családja egyenes vonalak.
A második eset által leírt egyenlettel
Keresse meg a megfelelő paraméteres kifejezés y:
A p paraméter elhagyható a képletek az x és y. A figyelem az utolsó egyenletet a téren, és felvenné őket, ezt kapjuk:
A kapott expressziós az egyenlet egy sugarú kör 1, található a származási. Így egy különleges megoldást jelentenek az egység kör síkjában xy, amely a borítékot a család egyenes vonalak.
- NS Piskunov "Megkülönböztető és integrálszámítás", Volume Two "Nauka", Budapest 1985
- E. Kamke. Handbook of közönséges differenciálegyenletek. M. Science 1976.
- Információforrások az interneten.
PAGE \ * MERGEFORMAT 19