A kúpos szakaszok elmélete
Elődeihez képest az Apollonia innovációját különösen a közösségben kifejezte, amellyel közeledett a témához. Először is, Apollonius meghatározta a kúpszakaszokat szakaszokként egy síkban, amely nem kell merőleges a kúp generátorára. Emellett az Apollonius, mint már említettük, a hiperbola második ágát is figyelembe vette, és ehhez figyelembe vette, hogy a kúp két üregből áll. Erre azért volt szükség, hogy az elméletek megegyezzenek a szükséges közösséggel - különben túl sok kivételt kellene megadnunk. Így a parabola megszűnt, csak egy eldugott kúp szakaszának, az ellipszis akut szögű, és a hiperbola elakad. Sőt, Apollonius tekinthető nemcsak egy köralakú kúp (vagyis azok, amelyekben a merőleges csökkent a felső, áthalad a központ a bázis), de önkényes és körkúpok.
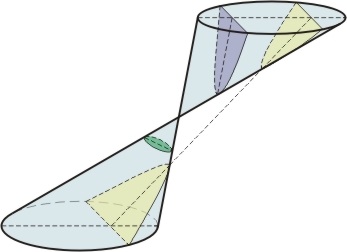
Ábra. 1. Apollonium kónuszos részei
Apollonius azt mutatta, hogy tetszőleges kúp keresztmetszeti síkban vezető csak e három típusú görbék (kivéve néhány degenerált esetben, például, amikor a keresztmetszet tartalmaz egy pár egymást metsző vonalak). Ez az, amiért meg kellett változtatni a terminológia: ahelyett, hogy „egy négyszögletes keresztmetszetű (akut, tompaszög) kúp” Apollonius bevezette a „parabola”, „ellipszis”, „túlzó”. Az utolsó leckében láttuk, hogy ezek a kifejezések kapcsolódnak az egyenletek ("tünetek") formájához, amelyek meghatározzák ezt a szakaszt. Apollonius megmutatta, hogy a koordináták közötti összefüggés, melyet e szakasz tünetei mutatnak:
y 2 = 2 px a parabola esetében,
y 2 = 2 px - (p / a) x 2 az ellipszishez,
y 2 = 2 px + (p / a) x 2 a hiperbóra,
nem változik, ha az abszcisza tengelyét nemcsak a kúpszakasz tengelye veszi.
Itt szükség van egy új kifejezés bevezetésére. Az ellipszis vagy a hiperbola átmérője olyan szegmens, amely ellipszis vagy hiperbola középpontján halad át. (Remélem, megérti, mi a központja túlzás azt közepén szimmetria - a metszéspont a aszimptotákkal). És az átmérője a parabola van olyan egyenes tengelyével párhuzamosan a parabola (azaz metsző parabola egyetlen ponton). Tehát, Apollonius azt mutatta, hogy a tünet a kúpszelet lesz ugyanolyan, ha az x tengelyen egy tetszőleges átmérője, a kúpos szakasz és a y-tengely - a tangens egyik végén ennek az átmérője. Így ezek nem lesznek téglalap alakú koordináták: az abszcisszák az átmérő szegmensei, és az ordináták a megfelelő érintővel párhuzamos félhangok. (A kúp alakú részek tulajdonsága, hogy az ezzel az érintéssel párhuzamos akkordok az adott átmérővel felére vannak osztva).
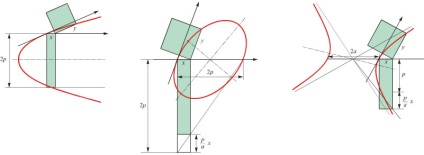
Ábra. 2. A kúpos szakaszok egyenleteinek formája az átmérő és a tangens által alkotott koordinátákban marad
Egy ellipszis és egy hiperbola esetében minden egyes átmérő esetében meg lehet határozni a konjugátumátmérőt, vagyis az átmérőt, amely párhuzamos az eredeti átmérő végein levő tangenciális átmérővel.
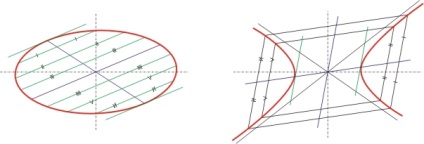
Ábra. 3. Konjugált átmérő
A konjugátum átmérõje fontos szerepet játszik az Apollonia elméletében. Különösen azt állítja, hogy:
- az ellipszis konjugátumátmérőinek négyzetek összege állandó;
- Az ellipszis konjugátumátmérőjén elhelyezett párhuzamos diagramnak állandó területe van.
Apollonius kiterjedten foglalkozik a kúpos szakaszok egyenletének formájával kapcsolatos kérdésekkel a két különböző átmérővel, különösen a konjugátummal egyező koordinátatengelyek vonatkozásában. A modern jelölésnél az ellipszis és a hiperbola egyenletei a konjugált átmérőkkel kapcsolatban (az ellipszis és a hiperbola úgynevezett központi egyenletei) így néz ki:
x 2 / a 2 + y 2 / b 2 = 1 (ellipszis),