A trigonometriai egyenlőtlenségek megoldása tangens, matematikai ismétléssel

3. Keresse meg a t értékének intervallumát. amely alatt az érintő az y = a egyenes vonal alatt helyezkedik el. Ennek az intervallumnak a bal határa mindig (-π / 2). és a jobb arctg a

4. Írja le a kettős egyenlőtlenséget a t argumentumra. figyelembe véve az érintő periódust T = π (t az abszcézák (-π / 2) és arctg a) között.

5. Fordított helyettesítést (visszatérünk az eredeti argumentumhoz), és kifejezzük x értékét a kettős egyenlőtlenségből, írjuk a választ numerikus intervallum formájában.

A trigonometrikus egyenlõtlenségek megoldása grafikusan megbízhatóan biztosítja a hibák ellen csak hibás grafikonok készítését.

Az y = tgx és y = 1 függvények grafikonjait hozzuk létre. Gondoljunk bele részletesen egy tangentum kialakításába. Készítsük elő az xOy koordinátasíkot az alábbiak szerint:

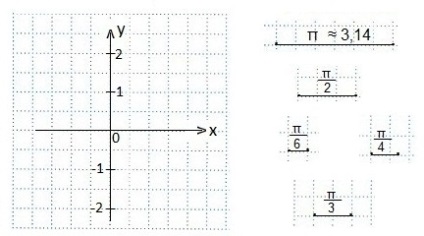
az egység szegmens két cellával egyenlő; mivel a π≈3,14 érték. akkor a π a vízszintes tengelyen az Oxet hat cellával lehet ábrázolni; fél π (ez π / 2) - három sejt. Egy sejt π / 6; egy és fél sejt π / 4; két sejt fog megfelelni az π / 3 argumentumnak.

Tudjuk, hogy a 90 ° érintő nem létezik, és mivel az érintő függvény periódusos, a legkisebb periódussal π. akkor nincs érintő (90 ° + πn). Ezt figyelembe vesszük a grafikon felépítésében és két aszimptotánkat. x = - π / 2 és x = π / 2.

Így a - π / 2-től π / 2-ig terjedő intervallumban az érintő "teljesít" minden értékét. Néhány szög érintkezési pontjának értékei és az érintőfunkció páratlan tulajdonsága (a grafikon szimmetrikus lesz a kiindulási értékhez képest), pontokat állítunk fel az előkészített koordináta síkban, amelyen keresztül a tangentust hozzuk létre.

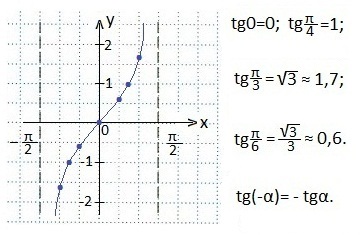
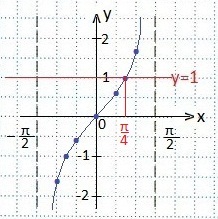
Az Ox tengelyével párhuzamosan húzzuk. magasabb egy egységnyi intervallummal (akár 2 cellával).

Az y = 1 egyenes metszi a tangenspontot a ponton a koordinátákkal (π / 4; 1).

Meghatározzuk az x értékek intervallumát, amelyre az egyenlőtlenség igaz, azaz. amelyen belül az érintő az y = 1 egyenes alatt helyezkedik el. Figyelembe vesszük, hogy az egyenlőtlenség nem szigorú, ezért az intervallum jobb oldali vége (π / 4) az egyenlőtlenségek megoldási sorában szerepel. A megoldást kettős egyenlőtlenség formájában írjuk. A választ rés formájában írják le.

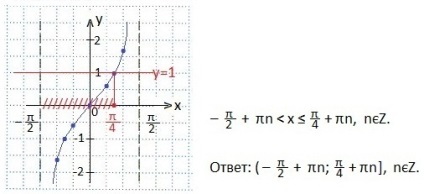
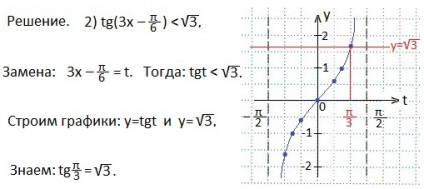
Vegye figyelembe a t értékének intervallumát. amelynél a tangenspontok pontjai az y = 1 egyenes pontjai alatt vannak. Írjuk ezt az intervallumot kettős egyenlőtlenség formájában. Aztán felülírjuk az eredeti érvet, és kifejezzük x-et. A választ rés formájában írják le.

Az értékek intervallumát jelöljük. amely szerint az egyenlőtlenség igaz. Van egy nem szigorú egyenlőtlenség, ami azt jelenti, hogy a t értékek intervallumának jobb vége is megoldást jelent az egyenlőtlenségre. Visszatérünk az eredeti érveléshez, és kifejezzük az x értéket. A válasz az x változó értéktartományában kerül megírásra.

Kapcsolódó cikkek